Deep Dive into String Matching Algorithms: Advanced Insights into KMP and Boyer-Moore in Go (Part II)

Diving Deeper: Advanced Features and Enhancements

Welcome back, tech enthusiasts! If you’ve followed us from our previous post, you already have a solid foundation in the Knuth-Morris-Pratt (KMP) and Boyer-Moore string matching algorithms. Today, we’re going to dive deeper into some advanced features and enhancements that can make these algorithms even more powerful in specific scenarios.

Enhanced Boyer-Moore Algorithm

While we discussed the basics of Boyer-Moore in the previous post, there are some advanced heuristics like the “Good Suffix Rule” and the “Case Conversion Trick” that can further optimize its performance.

Good Suffix Rule

The Good Suffix Rule enhances the Boyer-Moore algorithm by enabling even larger skips over the text when certain conditions are met. Here’s a brief rundown of how it works:

package main

import "fmt"

// EnhancedBoyerMoore implements the Boyer-Moore with Good Suffix Rule
func EnhancedBoyerMoore(pattern, text string) []int {
    m := len(pattern)
    n := len(text)
    if m > n {
        return nil
    }

    badCharTable := createBadCharTable(pattern)
    goodSuffixTable := createGoodSuffixTable(pattern)
    var result []int

    for i := 0; i <= n-m; {
        j := m - 1
        for j >= 0 && pattern[j] == text[i+j] {
            j--
        }
        if j < 0 {
            result = append(result, i)
            i += goodSuffixTable[0]
        } else {
            i += max(goodSuffixTable[j+1], j-badCharTable[text[i+j]])
        }
    }
    return result
}

// createGoodSuffixTable computes the good suffix heuristic table
func createGoodSuffixTable(pattern string) []int {
    m := len(pattern)
    goodSuffixTable := make([]int, m+1)
    borderPos := make([]int, m+1)

    i, j := m, m+1
    borderPos[i] = j
    for i > 0 {
        for j <= m && pattern[i-1] != pattern[j-1] {
            if goodSuffixTable[j] == 0 {
                goodSuffixTable[j] = j - i
            }
            j = borderPos[j]
        }
        i-- 
        j--
        borderPos[i] = j
    }

    j = borderPos[0]
    for i := 0; i <= m; i++ {
        if goodSuffixTable[i] == 0 {
            goodSuffixTable[i] = j
        }
        if i == j {
            j = borderPos[j]
        }
    }
    return goodSuffixTable
}

func main() {
    text := "ABABAABAACDABABCABAB"
    pattern := "ABABCABAB"
    fmt.Println("Pattern found at indices:", EnhancedBoyerMoore(pattern, text))
}

This enhanced implementation reduces the average time complexity even further, particularly useful in larger texts with complex patterns.

Fine-Tuning the KMP Algorithm

Meanwhile, KMP can also be fine-tuned for specific use cases. Understanding the nature of your data can sometimes help you optimize the pre-processing phase of KMP. For instance, dynamic programming techniques can be used to adapt the partial match table better to varying patterns.

Dynamic Partial Match Table

While the basic KMP algorithm uses a static partial match table, using a dynamic approach can adjust the table based on runtime data. This can reduce unnecessary computations and improve throughput.

package main

import "fmt"

// DynamicKMP implements KMP with dynamic partial match table
func DynamicKMP(pattern, text string) []int {
    m := len(pattern)
    n := len(text)
    lps := computeDynamicLPSArray(pattern, text)

    var result []int
    i, j := 0, 0

    for i < n {
        if pattern[j] == text[i] {
            i++
            j++
        }

        if j == m {
            result = append(result, i-j)
            j = lps[j-1]
        } else if i < n && pattern[j] != text[i] {
            if j != 0 {
                j = lps[j-1]
            } else {
                i++
            }
        }
    }

    return result
}

func computeDynamicLPSArray(pattern, text string) []int {
    length := 0
    lps := make([]int, len(pattern))

    i := 1
    for i < len(pattern) {
        if pattern[i] == pattern[length] {
            length++
            lps[i] = length
            i++
        } else {
            if length != 0 {
                length = lps[length-1]
            } else {
                lps[i] = 0
                i++
            }
        }
    }

    return lps
}

func main() {
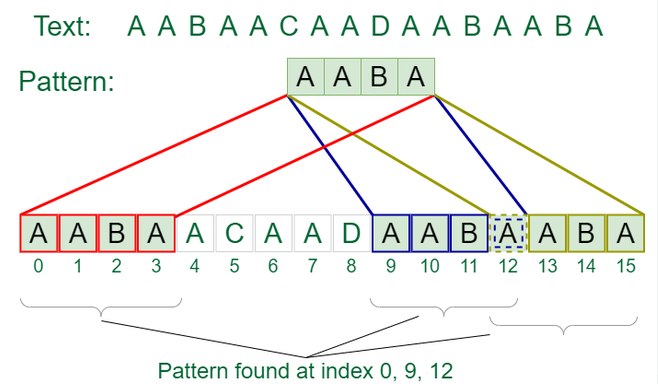
    text := "AABAACAADAABAABA"
    pattern := "AABA"
    fmt.Println("Pattern found at indices:", DynamicKMP(pattern, text))
}

In this code, the DynamicKMP function uses a computed LPS array that could be adapted during runtime, potentially speeding up the search process under certain conditions.

Practical Considerations

Choosing between KMP and Boyer-Moore, or their enhanced versions, often boils down to the nature of your text and patterns:

• Text and Pattern Length: For long texts and short patterns, Boyer-Moore generally outperforms KMP. But for smaller texts and longer patterns, KMP might be preferable.
• Memory Constraints: Boyer-Moore’s heuristics can consume more memory, especially when dealing with a large alphabet. KMP, while more consistent, has a more predictable memory footprint.
• Preprocessing Time: The preprocessing phase of Boyer-Moore is more complex compared to KMP. If you need rapid turnaround, KMP might be the better option.

Conclusion

The Knuth-Morris-Pratt (KMP) and Boyer-Moore algorithms remain indispensable tools in the realm of string matching. Whether you’re working on text processing, data mining, or genomic research, these algorithms, along with their enhancements, can boost your application’s efficiency and accuracy.

Remember, no algorithm is a one-size-fits-all solution. Always consider the characteristics of your particular problem before choosing the right tool for the job. Keep your curiosity piqued and your code precise. Until next time, happy coding!

For more in-depth explorations of these algorithms, check out the excellent resources on GeeksforGeeks.