Sorting Algorithms Face-Off in Python: QuickSort vs. MergeSort
Hello, tech enthusiasts! Today, we’re diving into the fascinating world of sorting algorithms with a showdown between two giants: QuickSort and MergeSort. These algorithms are fundamental in computer science and have practical applications in various domains. If you’re passionate about Python and want to optimize your sorting tasks, this post is tailor-made for you!
Understanding Sorting Algorithms
Sorting is at the heart of many applications, from searching data to optimizing algorithms. QuickSort and MergeSort are two efficient sorting algorithms that offer different approaches to solve the same problem—organizing elements in a list systematically.
QuickSort: The Divide and Conquer Champion
QuickSort is a Divide and Conquer algorithm. It picks an element as a pivot and partitions the array around the pivot. The key processes involved in QuickSort include:
1. Choose a Pivot – Typically, the pivot can be any element; however, often the first, last, or middle element is chosen.
2. Partitioning – Rearrange elements so those less than the pivot come before it, and those greater come after it.
3. Recursion – Recursively apply the above steps to the sub-arrays formed by partitioning.
Here is a Python implementation of QuickSort:
def quicksort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quicksort(left) + middle + quicksort(right)
# Example usage
print(quicksort([3, 6, 8, 10, 1, 2, 1]))
QuickSort is favored for its average-case complexity of O(n log n). However, its worst-case time complexity is O(n^2), which can happen if the pivot elements are not chosen wisely.
MergeSort: The Reliable Organizing Wizard
MergeSort is another Divide and Conquer algorithm, but it works by repeatedly breaking down a list into two halves until each segment has one element. The steps include:
1. Divide – Split the list into halves.
2. Conquer – Sort each half.
3. Merge – Combine the sorted halves into a single sorted list.
Here’s a Python implementation of MergeSort:
def mergesort(arr):
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left = mergesort(arr[:mid])
right = mergesort(arr[mid:])
return merge(left, right)
def merge(left, right):
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result.extend(left[i:])
result.extend(right[j:])
return result
# Example usage
print(mergesort([3, 6, 8, 10, 1, 2, 1]))
MergeSort has consistent performance with a time complexity of O(n log n) in all cases. It’s stable and works well with large datasets.
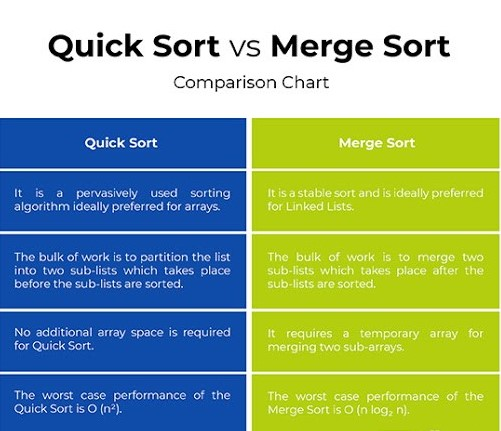
Face-Off: QuickSort vs. MergeSort
These two algorithms have their own strengths and weaknesses. Let’s explore a side-by-side comparison to determine when to use which:
| Criteria | QuickSort | MergeSort |
|---|---|---|
| Time Complexity (Average) | O(n log n) | O(n log n) |
| Time Complexity (Worst-Case) | O(n^2) | O(n log n) |
| Space Complexity | O(log n) | O(n) |
| Stability | No | Yes |
| Method | In-place | Out-of-place |
| Best Use Case | General-purpose, when space is limited | Stable sort required, large datasets |
Which One Should You Choose?
The choice between QuickSort and MergeSort depends on the specific requirements of the problem at hand:
QuickSort:
– Ideal for average cases where you need efficient in-place sorting.
– Suitable when memory space is a constraint since it has low space overhead.
MergeSort:
– Perfect for stable sorting needs, where the order of equal elements matters.
– Reliable for consistently good performance, especially with large datasets despite its higher space complexity.
Conclusion: Embrace the Power of Sorting
Both QuickSort and MergeSort are powerful and efficient sorting algorithms with their own sets of advantages. Your selection should align with your problem’s requirements—whether you prioritize in-place operations or stability and consistency.
Keep exploring the fascinating world of algorithms! They are not just about solving problems but also about understanding the broader landscape of computing.
For further reading on algorithm optimization, check out [this fantastic article](https://www.geeksforgeeks.org/sorting-algorithms/) which dives deeper into various sorting algorithms.
Don’t miss out on our other insightful articles on technology and development over at Sesame Disk Blog.
Happy coding, and may the best algorithm be with you! ?


